|
NFEモデルとは逆に,局在軌道からスタートしていこうというのがこのTight-Binding approximation(以下TB)です. 日本語では強結合近似というそのままの名前が付いています. これはどのようなものかというと,化学で言うところのHückel近似に,波数空間の考えを 組み合わせたもの,とでも言えばよいのでしょうか. 以下一番簡単な例として,高度な近似を一切含まない,一番簡単な形で説明させていただきます. 実は分子性導体,特にTTF系分子性導体の場合,Hückelで分子軌道を求めて,その分子軌道を もとにしてこの一番簡単なTBを用いるだけで,かなり現実の系に一致する結果が得られています. というかより高度な近似を入れれば入れるほど合わなくなっていくという不思議な状況が.
まず,TBでは各サイトの原子軌道(or 分子軌道)は変化しないと考え,さらに1電子
近似を用います.
この時,各サイトでのクーロン積分(Hückelで言うところのα),およびサイト間を
飛び移ることに相当するトランスファー積分(共鳴積分,Hückelで言うところのβ)
で電子のエネルギーが求まるわけです. 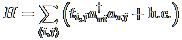 バルク固体の場合,サイト数が無限になりこのままの表記では面倒なので,波数空間での 表示に変換してやります. 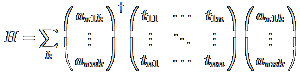 ここでnは単位格子中のサイトの数です. この変換でハミルトニアンが簡単になるのは,結晶中など周期的なポテンシャル中の電子状態が Blochの定理により平面波をポテンシャルと同じ周期を持つ関数で変調したものとして 表せることによります.つまりこれにより,単位格子(例えばa方向に)ずれた分子の 波動関数は,元の格子の同じ分子の波動関数に位相因子exp(ika)をかけたものに等しいわけです. さて,これだけではちょっとわかりにくいので,実際の例で説明しましょう. 下図のような,単位格子中に分子1(黄緑),2(オレンジ)を含む導体があったとします.またそれぞれの分子間の トランスファー積分は図中に直線で示してあり.その値はp-tであるとします. さらに簡単のためこの物質は二次元伝導体であるとし,紙面垂直方向への電子の移動は無視します. また下図では注目しているある単位格子と,隣接する8つの単位格子が描いてあります. 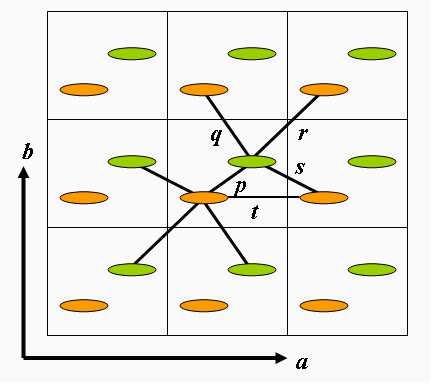  となります. 同様に他の値も計算してやると,  が得られます.ここでαiは分子iのクーロン積分で,全分子が 同じ場合は省略できます. これをハミルトニアンに入れ,各波数に対する固有値を求めてやれば それがその波数の電子のエネルギーであり,波数を変えながら計算してやることで バンド構造を書くことが可能となります. このように,分子間相互作用による分子軌道の変形やらが一切 入っていないにもかかわらず分子性導体で良くバンド構造を再現できるのは,分子性 導体においてはその軌道間の重なりが非常に小さく,あまり軌道の形に影響を与えないというのが 効いているのだと思われます. ただし,逆にその場合電子が移動しにくいわけで,電子間反発がかなり効いてくることから, 各サイトに電子が1つあるような系の場合,Mott絶縁化を示すなど単純なTBからは ずれてくることもあります. まあ,不思議なことにそういうずれてくる系は数が少ないわけですが. |